How to Implement a Binary Search Tree in JavaScript – Part 1

Before getting our hands dirty, let’s make sure we are on the same page by defining the core concepts of a Binary Search Tree (BST). If you’re already comfortable with the concepts you can go straight to the coding part

What is a Binary Search Tree ?

In simple terms, A Binary Search Tree (BST) is a data structure that provides fast insertion, deletion, and lookup of its nodes (components).

What are the components and properties of a Binary Search Tree?

Components

Root node : the entry point of the tree. It has no parent.
Node : holds a value and may have:
- 0 child (leaf node)
- 1 child
- 2 children

Properties

Given a node X, its left child Y and its right child Z the following is always true:

     Y < X < Z

Here is a diagram to illustrate that: 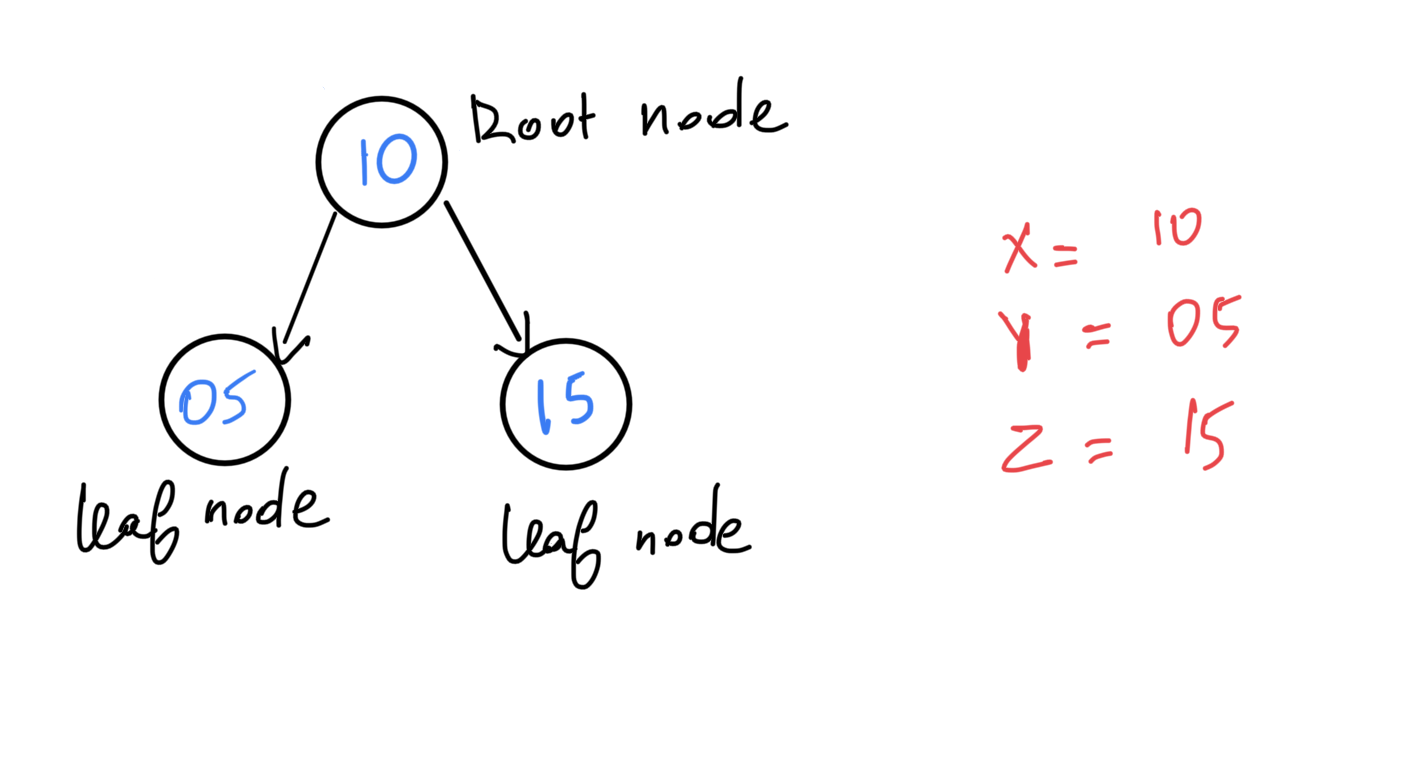diagram showing All nodes on the left side of a specific node will have a smaller value than the node, and all nodes on the right side will have a greater/bigger value than the node.

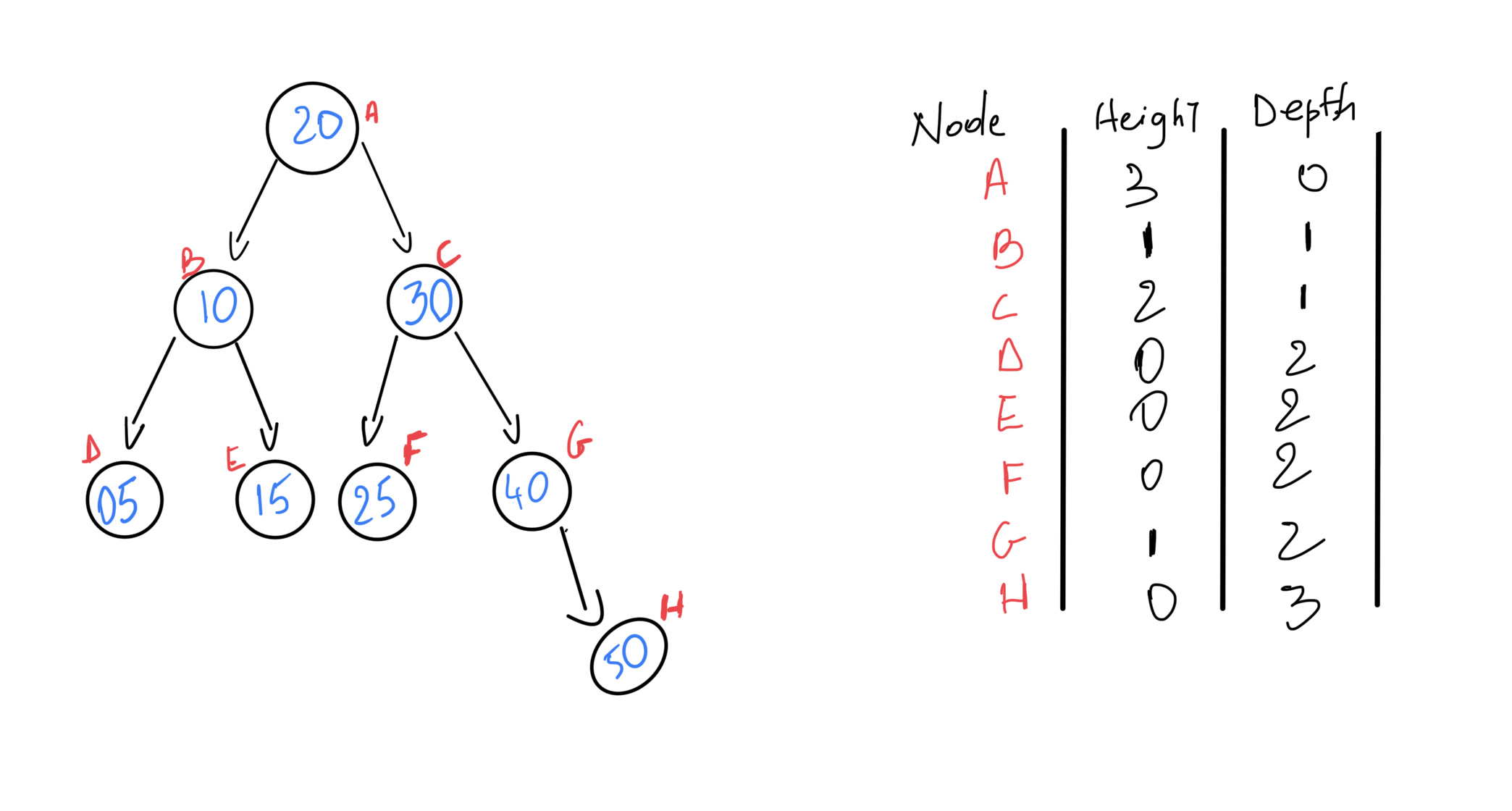
Depth : How far a specific node is from the root.
A good way to find it, is to count how many edges between the node and the root node.
Height : How far down the deepest leaf is from that node.

To find the height of a node you can use the following:

   1 + max(left-child-height, right-child-height)

it reads one plus the maximum between left child’s height and right child’s height. The height of a leaf node is 0 a binary search tree diagram with label and a second diagram showing height and depth of each node

What are the different types of binary search Trees ?

Full: Every node has either 0 or 2 children.
Example:
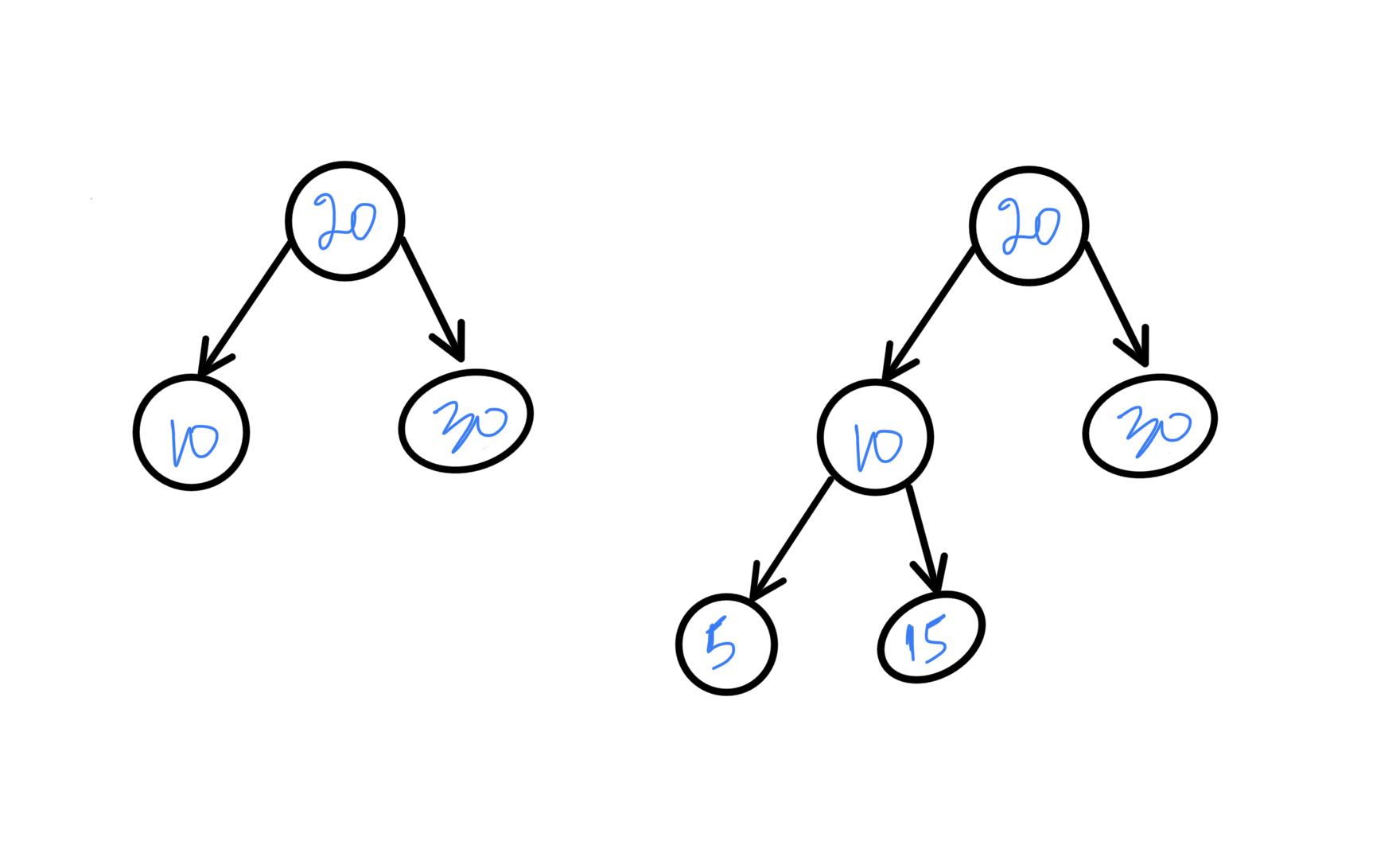
Complete : All levels are completely filled except the last one, which is left sided, or filled from left to right. The following diagram illustrates that:

diagram of a complete binary tree and an incomplete binary tree

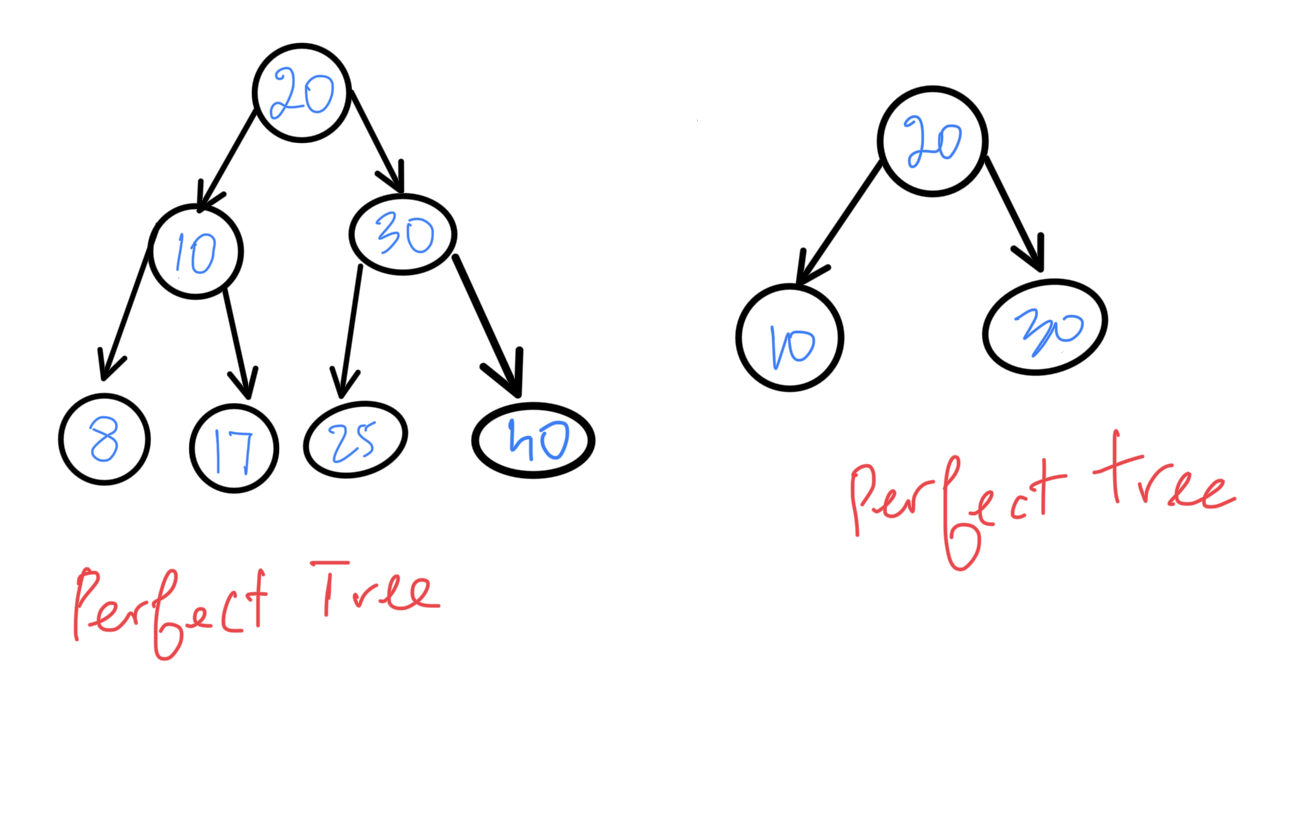
Perfect : All internal nodes are completely filled and all the leaf nodes are at the same depth. Example: diagram of a perfect binary tree

Degenerated or skewed: Each node has only one or 0 child Example: diagram of a degenerated binary Search tree

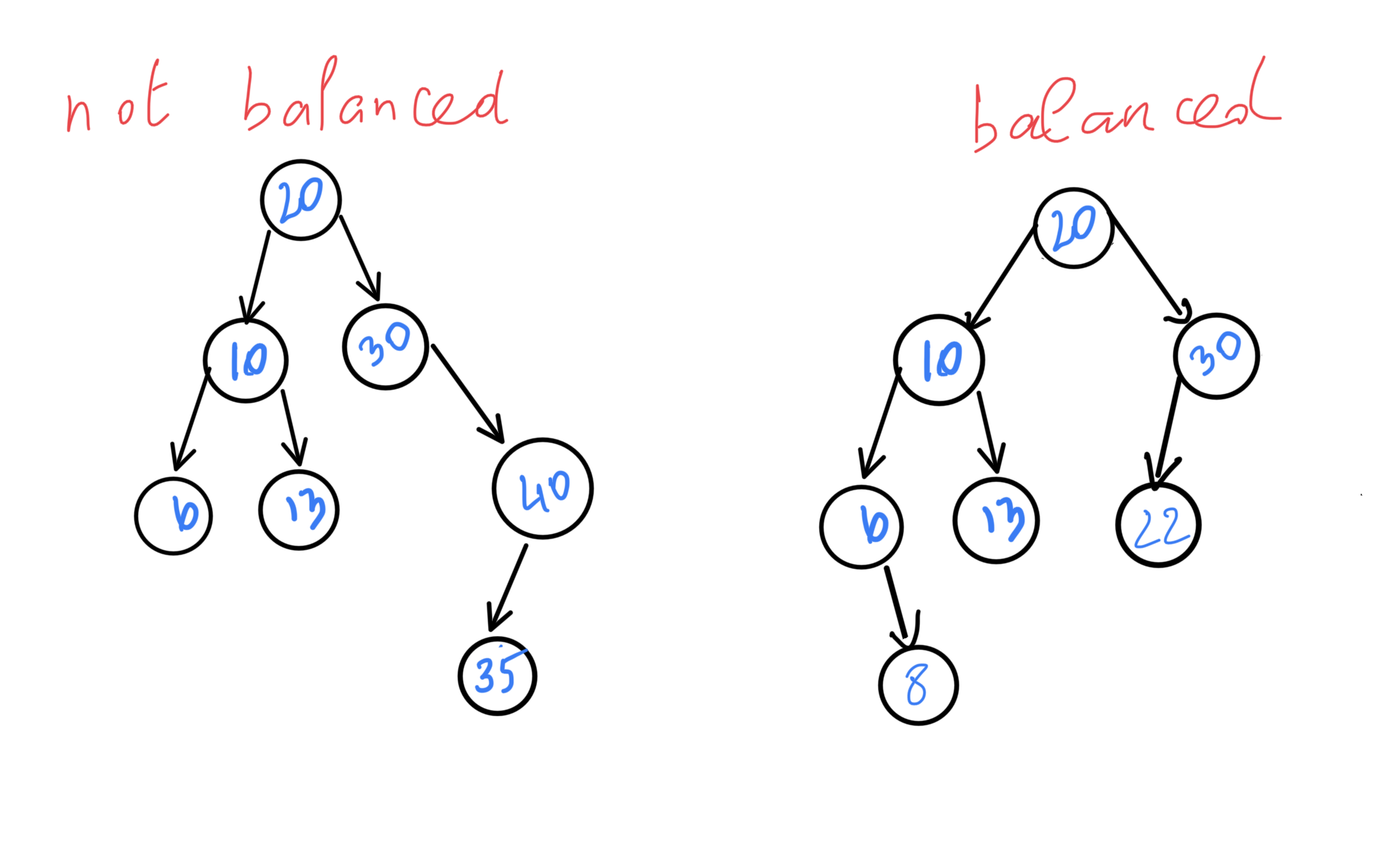
Balanced : The height difference between the left and right subtrees of every node is at most 1
Keeping a tree balanced is a very important concept of (BSTs), because in the worst case scenario a tree can degenerate into a linked list resulting in an 0(n) time complexity. diagram of a balanced binary Search tree

What are the use cases of a Binary Search Tree ?

Databases : for indexing datasets efficiently.
File System : Organizing folder
Search algorithms : Often used as a foundation of many searching and sorting operations

Now that we know the core concepts let’s move to the coding implementation in part 2 Here