How to Implement a Binary Search Tree in JavaScript – Part 2

Building on the theoretical concepts from Part 1, this post will guide you through the practical implementation of a Binary Search Tree in JavaScript. If you landed on Part 2 without reading Part 1, you can read it Here! .

How to insert data in a Binary Search Tree?

Before we write the insert method, we need to define the Binary Search Tree structure. Data structures are abstractions, so your implementation may differ from mine. What matters is that it behaves correctly and efficiently. A vital aspect of software is that it does what it is supposed to do in an efficient way. I’ll mostly use recursion instead of an iterative approach and no duplicate values will be allowed.

We’ll start with two classes:

• TreeNode: represents a single node
• BinarySearchTree: represents the full tree and contains the logic (like insert, search, and delete)

Defining the TreeNode class

This class models the nodes in our tree. Each node stores an integer value (key) and references to its left and right children.

class TreeNode {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

Defining the BinarySearchTree Class

This is the main class that manages the tree. The constructor tracks the root and the number of nodes (length). We’ll then add methods to insert, search, and remove nodes.

class BinarySearchTree {
  constructor() {
    this.root = null;
    this.length = 0;
  }

  // Our methods will go here
}

With the basic structure in place, Let’s implement the insert method.

Insertion

What steps the method need to take to accomplish the end goal ?

• check if the (key) argument is valid
• check if the tree is empty
  • yes ? assign root
  • No ? find our new node parent
• place node if not a duplicate
• increase length if success
• return either true or false for success or failure

Based on what my insert method needs to do I will extract the process of finding the node Parent into its own method for readability, and separation of concerns.

We’ll have two methods:

• findNewNodeParent: finds a new node parent
• insert : Main logic for insertion goes here.

Finding new node parent code.

   findNewNodeParent(currentNode, key){
    if(key === currentNode.key ) return false; // node exists already, no duplicate
    if(key > currentNode.key && currentNode.right){
        // move right
        return this.findNewNodeParent(currentNode.right, key)
    }else if(key < currentNode.key && currentNode.left){
        // move left
        return this.findNewNodeParent(currentNode.left, key);
    }
    // A parent node is found, base case
    return currentNode;

   }

Note the use of the return keyword here. This is essential for propagating the result back up the recursive call stack, ensuring the correct parent node is returned to the insert method.

Insert code

 insert(key) {
    if (!Number.isInteger(key)) return false;
    // add root
    if (!this.length) {
      let node = new TreeNode(key);
      this.root = node;
    } else {
      // find where to place node;
      const nodeParent = this.findNewNodeParent(this.root, key);
      // return false when duplicate value
      if (!nodeParent) return false;
      // place node based on key value
      const newNode = new TreeNode(key);
      if (key > nodeParent.key) {
        nodeParent.right = newNode;
      } else {
        nodeParent.left = newNode;
      }
    }

    this.length++;
    return true;
  }

Testing insert Method

const bst = new BinarySearchTree();
bst.insert(20);
bst.insert(30);
bst.insert(10);
console.log(bst.root);

Output of the previous snippet:

Next We’ll implement a way to search for a specific node.

How to find data in a Binary Search Tree?

Searching

Our find method will return null when a node is not found, and will return the entire node when found. Let’s break it down:

• check if a tree is empty
  • yes ? return null for node not found;
  • no ?
    • move left or right based on key value
  • found ? return node
  • not found ? return false

    find(key, currentNode = this.root){
        if(!currentNode) return null; // base case 1, tree empty or node not found.
        if(currentNode.key === key) return currentNode; // base case 2 node is found

        if (key < currentNode.key) {
            return this.find(key, currentNode.left);
        } else {
         return this.find(key, currentNode.right);
        }
    }

Testing the find method

const bst = new BinarySearchTree();

bst.insert(20);
bst.insert(30);
bst.insert(10);

console.log(bst.find(30));
console.log(bst.find(100));

Output of the previous code snippet

How to find the Minimum and Maximum value in a Binary Search Tree?

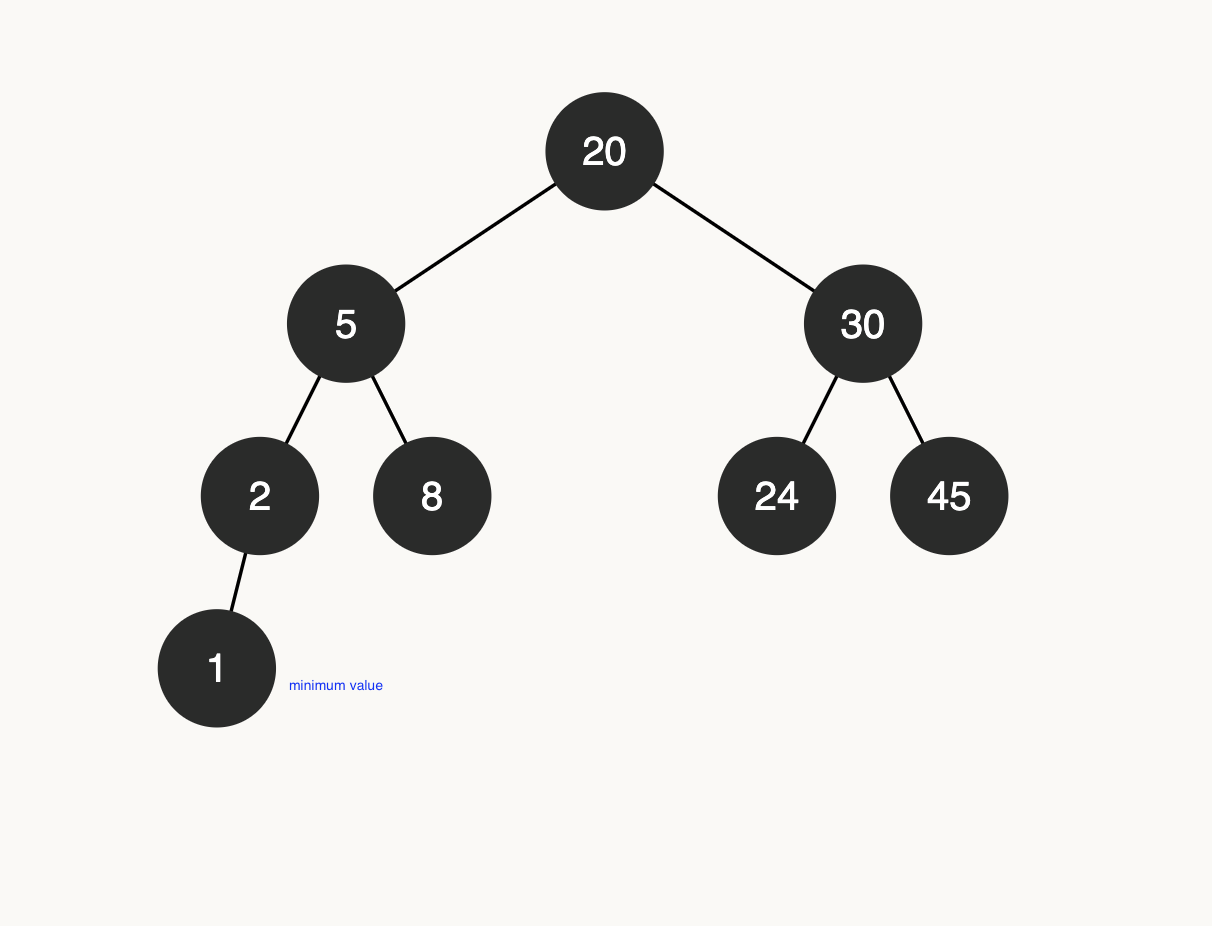
Since all nodes on the left side of the root are smaller than the root, the minimum will always be the deepest leaf on the left side of the root. As an example, In the Following diagram the minimum is 1

What steps the method need to take to accomplish the end goal ?

• Check if the Tree is empty
  • yes ? return null
  • no ? move all the way to the left until we reach the deepest leaf and return it.

Implementation

    getMin(currentNode = this.root){
        if(!currentNode) return null; // base case
        if(currentNode.left){
            return this.getMin(currentNode.left);
        }else{
            return currentNode; // min is found
        }

    }

getMin implementation testing

console.log(bst.getMin().key); // expected output : 10

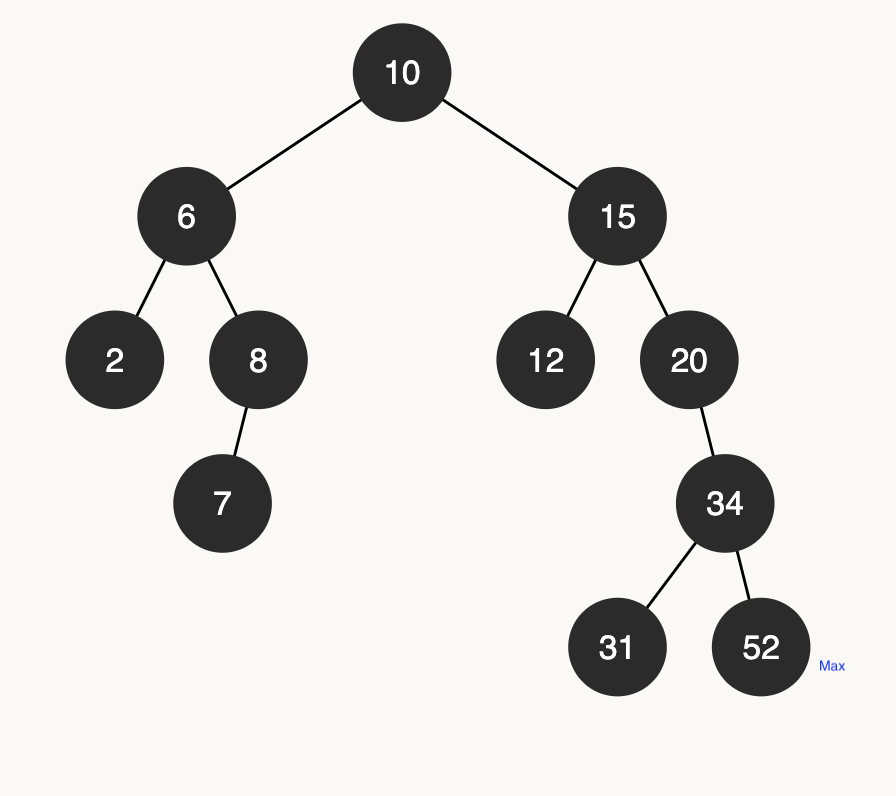
The next method getMax() represents the bigger value in the tree, the maximum. The deepest leaf node on the right side of the root. In the following tree, the maximum is 52.

getMax() implementation

    getMax(currentNode = this.root){
        if(!currentNode) return null;
        if(currentNode.right){
            return this.getMax(currentNode.right)
        }else{
            return currentNode
        }

    }

getMax() output example

// previous insert and initialization goes here
console.log(bst.getMax().key); // expected output : 30

How to traverse a Binary Search Tree ?

There are essentially 2 main traversal methods:

Breadth-First search (BFS)

In a BFS the nodes are visited by level. Let’s look at the following example and determine the output of a Breadth First Search (BFS).

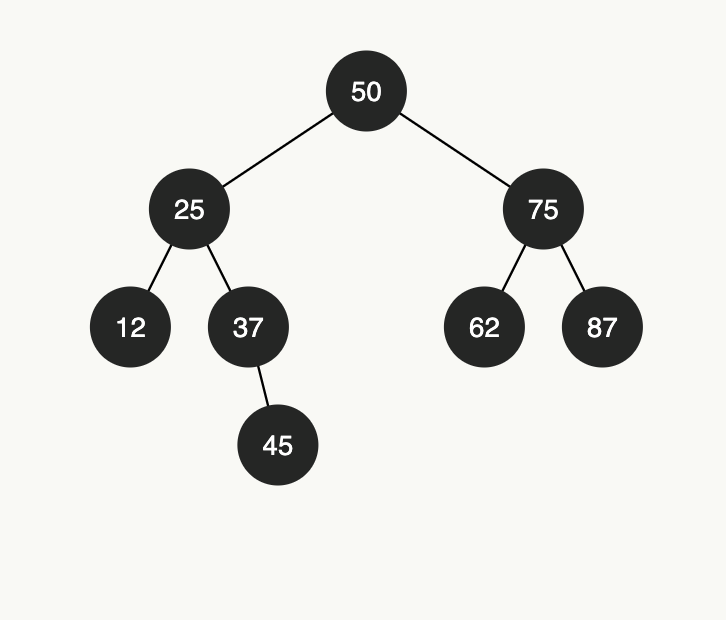
The nodes are visited by level from left to right so we get the following sequence: [50, 25, 75, 12, 37, 62, 87, 45 ]

Depth-First Search

DFS, has 3 sub-categories that we’ll be implementing:

• In-order Traversal : nodes are visited in an ascending order, the left child, the node, then the right child.
• Post-order Traversal, the children are visited before the node, it goes left child, right child, then node.
• Pre-order traversal , the node is visited first then his children from left to right. Ideal for creating a copy of the tree.

Tree sample

DFS results

• In-order result : [12, 25, 37, 45, 50, 62, 75, 87]
• Post-order result: [12, 45, 37, 25, 62, 87, 75, 50]
• Pre-order result : [50, 25, 12, 37, 45, 75, 62, 87]

In-order Traversal

What steps the method need to take to accomplish the end goal ?

• Define the data structure that will hold the result.
• check if tree is empty
  • yes ? return []
• traverse left subtree and add nodes to data structure
• add root to data structure
• traverse right subtree and add nodes to data structure

  inOrderTraversal(node = this.root) {
    const inOrderArr = [];
    const traverseTree = (node) => {
      if(!node) return
      traverseTree(node.left);
      // push node's key to array
      inOrderArr.push(node.key);
      traverseTree(node.right);
    };
    traverseTree(node);
    return inOrderArr;
  }

inOrder output example

const bst = new BinarySearchTree();
bst.insert(20);
bst.insert(30);
bst.insert(10);
console.log(bst.inOrderTraversal()); // expected output [10,20,30]

Post-order Traversal

What steps the method need to take to accomplish the end goal ?

• Define the data structure that will hold the result.

• check if tree is empty

  • yes ? return[]

• traverse left subtree and add nodes to data structure

• traverse right subtree and add nodes to data structure

• add root to data structure

  postOrderTraversal(node = this.root) {
    const postOrderArr = [];
    const traverseTree = (node) => {
      if (!node) return ;
      traverseTree(node.left);
      traverseTree(node.right);
        // push node's key to array
      postOrderArr.push(node.key);
    };
    traverseTree(node);
    return postOrderArr;
  }

postOrder output example

const bst = new BinarySearchTree();
bst.insert(20);
bst.insert(30);
bst.insert(10);
console.log(bst.postOrderTraversal()); // expected output [10,30,20]

Pre-order Traversal

What steps the method need to take to accomplish the end goal ? Our preOrder method needs to print the root, his left subtree and right subtree.

  preOrderTraversal(node = this.root) {
    const preOrderArr = [];
    const traverseTree = (node) => {

      if (!node) return ;
      // push node's key to array
      preOrderArr.push(node.key);
      traverseTree(node.left);
      traverseTree(node.right);
    };
    traverseTree(node);
    return preOrderArr;
  }

preOrder output example

const bst = new BinarySearchTree();
bst.insert(20);
bst.insert(30);
bst.insert(10);
console.log(bst.preOrderTraversal()); // expected output [20, 10, 30]

Predecessor and Successor in a Binary Search Tree

Finding the predecessor or successor is a crucial step when deleting a node with two children in a Binary Search Tree. In this section, we’ll break down each concept, starting with a clear definition, then walking through the code implementation.

Predecessor

What is a Predecessor in a Binary Search Tree?
The predecessor of a node X for example in a BST, is the node that comes right before it in an in-order traversal. Meaning the node that has the biggest value that is smaller than node X.
Tree example

In the previous tree, taking a few nodes as examples We’ll get:

• 50’s predecessor is 45.
• 25’s predecessor is 12
• 75’s predecessor is 62

How to write the predecessor method?

   getPredecessor(key, currentNode = this.root, predecessor = null){
       if(!currentNode) return  predecessor; // no predecessor was found for Key.
       if(key < currentNode.key){
         return this.getPredecessor(key, currentNode.left, predecessor)
       }else if(key > currentNode.key){
        // current node might be the predecessor We keep track of it. and move right
        return this.getPredecessor(key, currentNode.right, currentNode)
       }else{
           if(currentNode.left)return this.getMax(currentNode.left); // maximum value in the left subtree

          return predecessor || null;

       }
   }

getPredecessor output example

const bst = new BinarySearchTree();
let data = [50, 25, 75, 12, 37, 62, 87, 45];
data.forEach((element) => bst.insert(element));

console.log(bst.getPredecessor(50));
console.log(bst.getPredecessor(25));
console.log(bst.getPredecessor(75));

Successor

What is a Successor in a Binary Search Tree?
A successor of a node in a Binary Search Tree is a node that comes right after the specific node in an in order traversal. Meaning, the smaller key value that’s greater than the current node’s.

Let’s reuse the previous tree as an example to determine the successor of a few nodes:

• 50’s successor is 62.
• 25’s successor is 37
• 75’s successor is 87

How to write the successor method?

  getSuccessor(key, currentNode = this.root, successor = null) {
    if (!currentNode) return successor; // no more tree to traverse return successor if found or null
    if (key > currentNode.key) {
      return this.getSuccessor(key, currentNode.right, successor);
    } else if (key < currentNode.key) {
      return this.getSuccessor(key, currentNode.left, currentNode);
    } else {
      if (currentNode.right) return this.getMin(currentNode.right); // minimum value in the right subtree

      return successor || null;
    }
  }

getSuccessor output example

const bst = new BinarySearchTree();
let data = [50, 25, 75, 12, 37, 62, 87, 45];
data.forEach((element) => bst.insert(element));

console.log(bst.getSuccessor(50));
console.log(bst.getSuccessor(25));
console.log(bst.getSuccessor(75));

Now, if I have to be honest I have been dreading the next section. Not because I do not know how to implement it, even though it is a bit challenging, but mostly because I need to figure out how to make it easy to grasp.

How to delete data in a Binary Search Tree?

Deleting a node in a Binary Search Tree, falls into 3 categories :

• node has no children (leaf)
• node has one child
• node has two children.

If you tried to guess the number of sub-methods, and said 3 you were close, and could definitely do so, but I particularly know I’ll need more than that. We’ll see why.

Leaf Node removal

The first scenario We’ll tackle is a leaf node. Let’s pull my previous tree example again.

Now if we are trying to delete the leaf node 12, left child of its parent 25, its parent left child needs to be null. The tree We’ll have is the following:

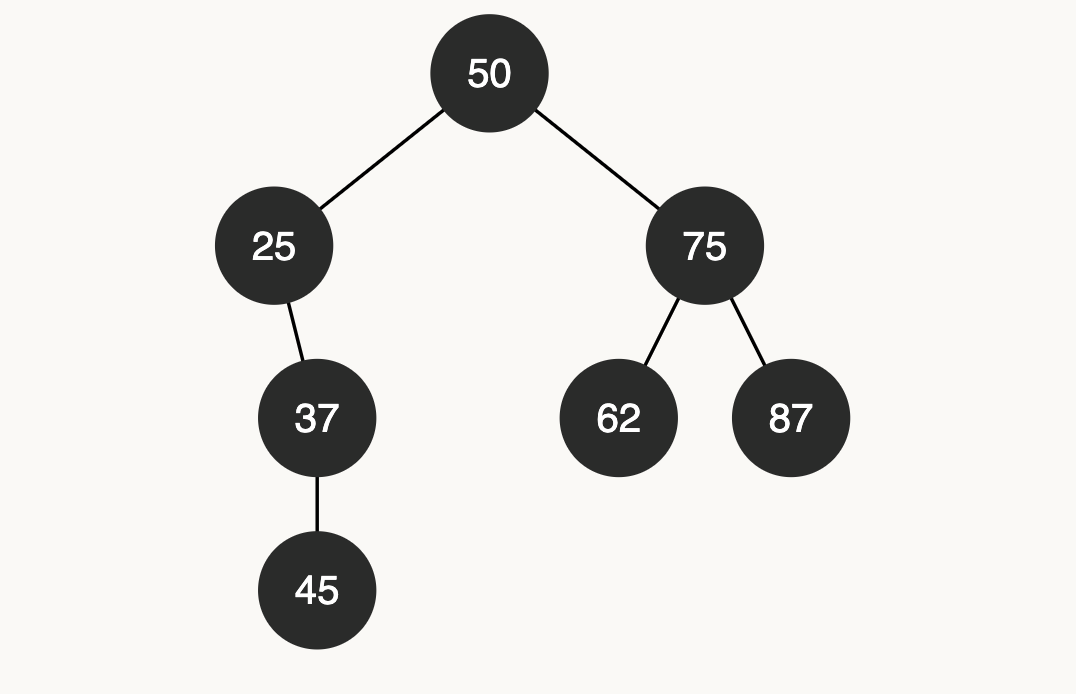
What steps the method need to take?

• IsNodeToDelete root ? :
  yes ?

  • assign root to null

• no ?
  isNodeToDelete a left child or right child ?
  Assign nodeParent child to null based on previous assertion

• decrease length

  deleteLeafNode(nodeParent, key) {
    // deleteLeafNode takes the node's to delete parent and the key
    if (!nodeParent && this.root.key === key) {
      // root is the node to delete
      this.root = null;
    } else if (nodeParent && nodeParent.right && nodeParent.right.key === key) {
      nodeParent.right = null;
    } else {
      // leaf node is a left child
      nodeParent.left = null;
    }

    this.length--;
    return true;
  }

Single-Child Node removal

Let’s look at the following tree, to get an idea of how our method will proceed.

In the previous tree if We were to delete the node 10, its parent 20 will need to have its left child becomes the child of 10 which is 15.
If We were to delete the node 15 its parent 10 will need to have its right child becomes the child of 15 which is 12.

   deleteSingleChildNode(nodeParent, key){
    // handle root case
    if(!nodeParent){
      this.root = this.root.left || this.root.right; // assigning root to become whichever child it has
    }else{
      if(nodeParent.left && nodeParent.left.key === key){
        // node to delete is the left child of the nodeParent
        nodeParent.left = nodeParent.left.left || nodeParent.left.right;
      }else{
        // node to delete is the right child of the nodeParent
        nodeParent.right = nodeParent.right.left || nodeParent.right.right;
      }
    }
    this.length--
    return true;

   }

Node with two children removal

This method can be implemented using either the predecessor, or the successor. Both approaches are valid and if correctly done, should maintain the Binary Search Tree’s properties. Our implementation will use the successor. Let’s look at the following tree :

Now, deleting a node with two children comes down to replacing the node with its successor. For example for the node 50 We need to replace it with its successor 62.
The successor will always have at most one child (0 or 1 ) if it has a child, it will always be a right child, and will take the successor spot in the deletion process.
Here’s an example to illustrate that: 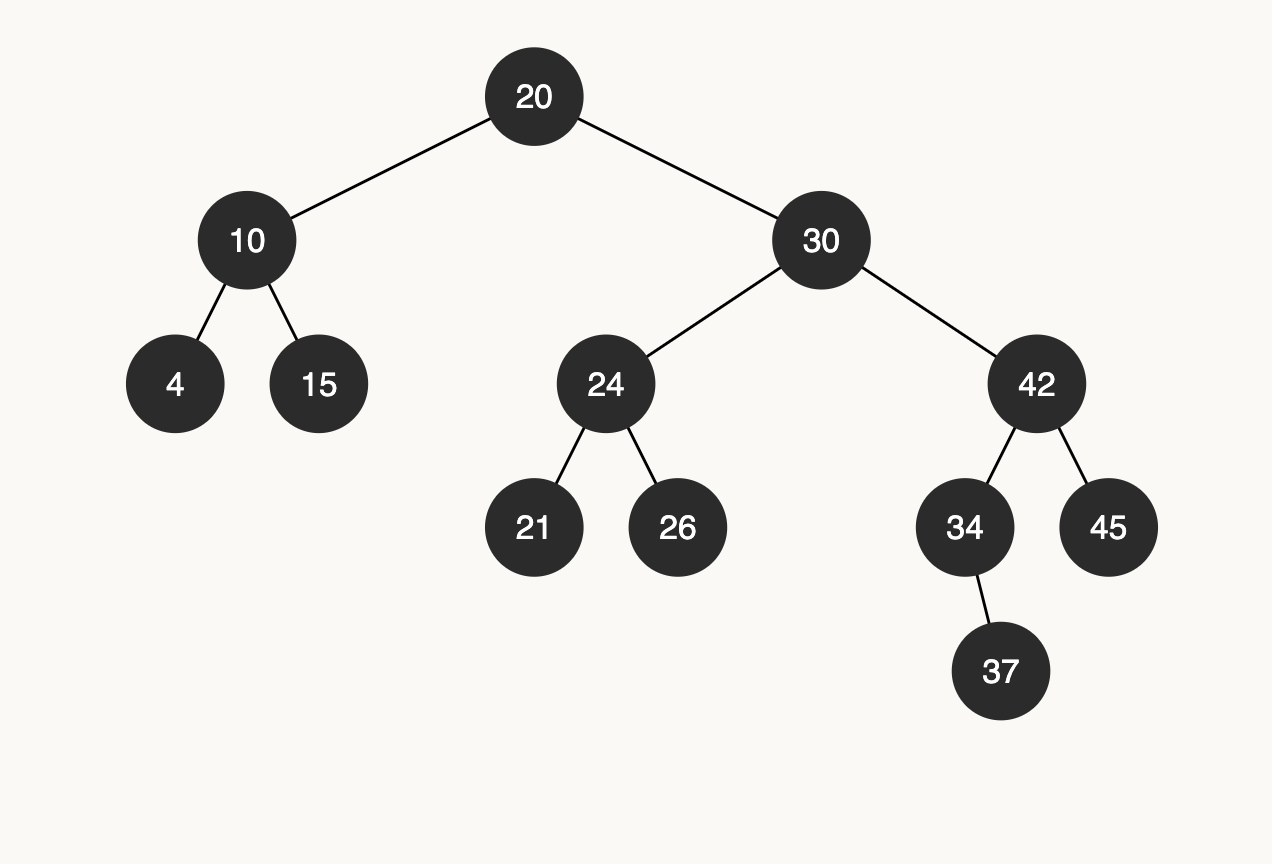If We were to delete the node 20 in that example 21 will be the successor so we need to replace 20 with 21. 21 has no children. Now let’s say we are trying to delete node 30, the successor here 34 has one child which is the right child, like we previously mentioned.

Let’s first create one helper method that will help us keep track of a node’s parent. If you’ve noticed the two previous method We wrote take a node’s parent as argument. Might as well implementing the code now. I also want to mention that, this could have been avoided if each node was keeping track of the parent on top of the left and right child. However most implementation do not keep track of the parent node. Remember abstraction.

  findNodeParent(key, currentNode = this.root, nodeParent = null){
    if(!currentNode)return false;
    if(key > currentNode.key){
      return this.findNodeParent(key, currentNode.right, currentNode)
    }else if(key < currentNode.key){
      return this.findNodeParent(key, currentNode.left, currentNode)
    }else{
      return nodeParent;
    }
  }

Now that We have our helper method Let’s break down our deleteNodeWithTwoChildren method.

• Find Successor,
• Find successor’s parent
• Does sucessor have a right child ?
  • yes ? right child takes its spot
• successor left child becomes node to delete left child
• successor right child becomes node to delete right child if node to delete is not the parent
• replace node with successor
• return successor;

Again We always replace a node with two children by its in-order successor: the minimum node in its right subtree.
Then we detach the successor from its old spot (lifting its right child if any) and splice it where the deleted node was.

     deleteNodeWithTwoChildren(nodeToDelete, nodeParent) {
    // let's start by getting the successor of the node to delete
    // minimum in right subtree calling getSuccessor will return the following line
    //if (currentNode.right) return this.getMin(currentNode.right);

    const successor = this.getMin(nodeToDelete.right);
    const successorParent = this.findNodeParent(successor.key);
    successor.left = nodeToDelete.left;


    if (successorParent && successorParent !== nodeToDelete) {
      successorParent.left = successor.right || null;
      successor.right = nodeToDelete.right;
    }

    if (!nodeParent) {
      this.root = successor;
    } else if (nodeParent.right === nodeToDelete) {
      nodeParent.right = successor;
    } else if (nodeParent.left === nodeToDelete) {
      nodeParent.left = successor;
    }

    this.length--;
    return successor;

  }

Let’s implement the main delete method

   delete(key) {
    if (!Number.isInteger(key) || !this.root) return false;
    // Getting the parent
    const parent = this.findNodeParent(key);
    // find the node to delete
    let nodeToDelete;
    if (this.root.key === key) {
      nodeToDelete = this.root;
    }

    if (parent && parent.left && parent.left.key === key) {
      nodeToDelete = parent.left;
    } else if (parent && parent.right && parent.right.key === key) {
      nodeToDelete = parent.right;
    }
    if (!nodeToDelete) return false;
    if (!nodeToDelete.right && !nodeToDelete.left) {
      return this.deleteLeafNode(parent, key);
    } else if (nodeToDelete.right && nodeToDelete.left) {
      return this.deleteNodeWithTwoChildren(nodeToDelete, parent);
    } else {
      return this.deleteSingleChildNode(parent, key);
    }
  }

Leaf node deletion output

const bst = new BinarySearchTree();
let data = [20, 10, 4, 15, 30, 24, 21, 26, 42, 34, 45, 37];
data.forEach((element) => bst.insert(element));
console.log(bst.delete(4)); // leaf node, also the minimum.
console.log(bst.getMin().key); // will give us the new minimum after deletion should be 10

Here’s our the tree look like now: 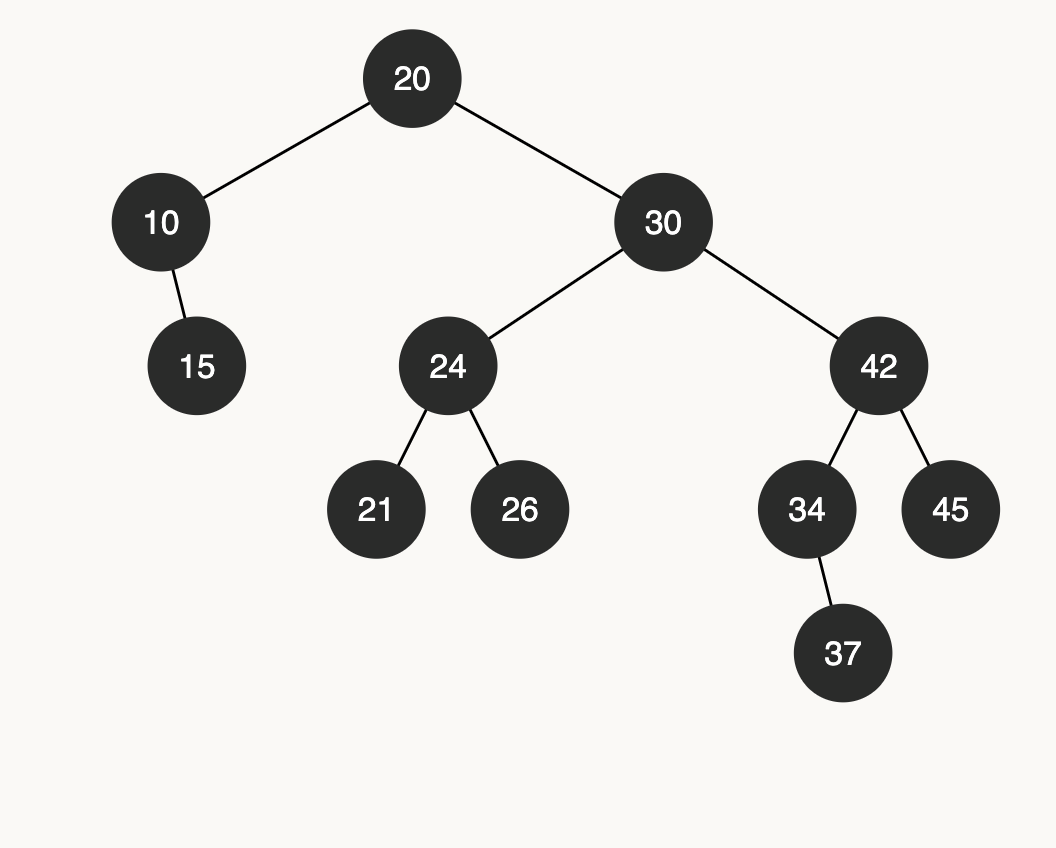Now Let’s delete node 10:

const bst = new BinarySearchTree();
let data = [20, 10, 4, 15, 30, 24, 21, 26, 42, 34, 45, 37];
data.forEach((element) => bst.insert(element));
console.log(bst.delete(4)); // leaf node, also the minimum.
console.log(bst.getMin().key); // will give us the new minimum after deletion should be 10
console.log(bst.delete(10)); // single child node deletetion
console.log(bst.getMin().key); // output will now be 15

output

Here is out the Tree looks like now:

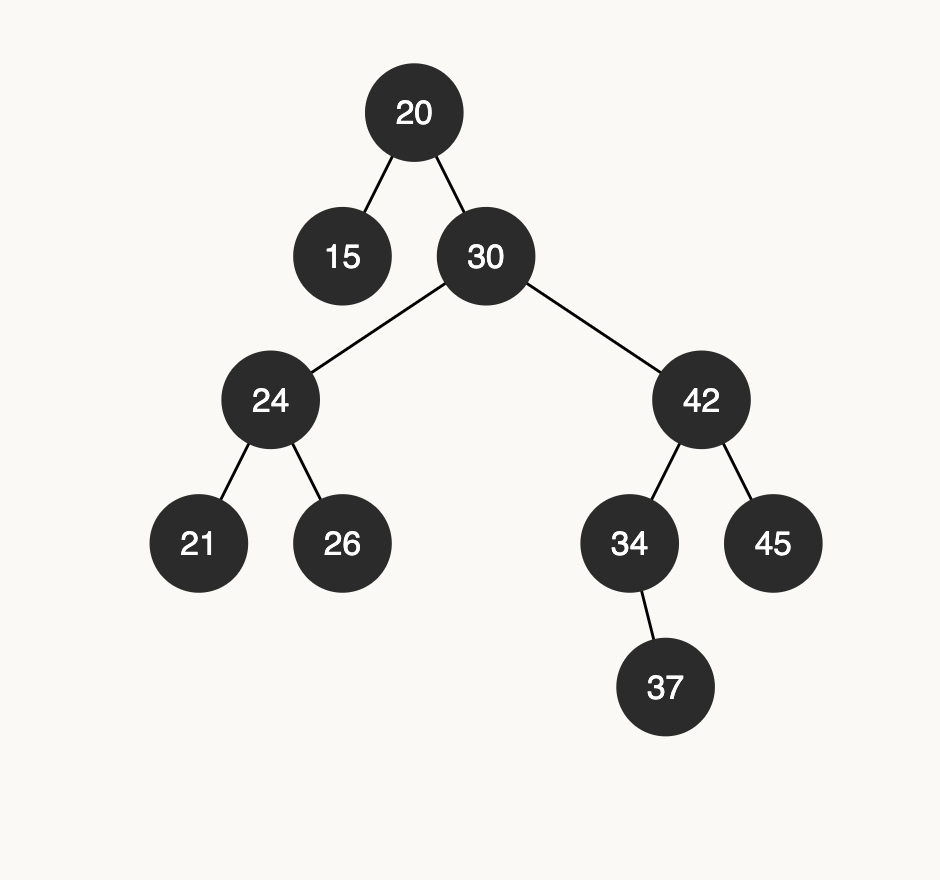
And to finish with the deletion let’s delete a node with two children 30

const bst = new BinarySearchTree();
let data = [20, 10, 4, 15, 30, 24, 21, 26, 42, 34, 45, 37];
data.forEach((element) => bst.insert(element));
console.log(bst.delete(4)); // leaf node, also the minimum.
console.log(bst.getMin().key); // will give us the new minimum after deletion should be 10
console.log(bst.delete(10)); // single child node deletetion
console.log(bst.getMin().key); // output will now be 15
console.log(bst.delete(30)); // two children node deletion here instead of true, we get the successor

Output
Here how the tree looks like:

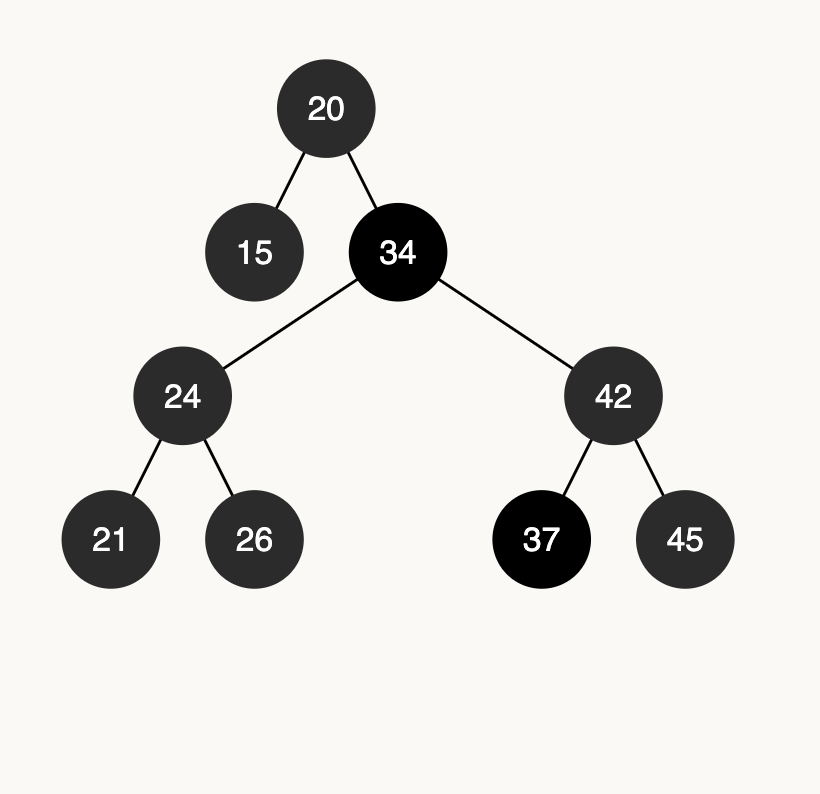
With that last output, We have visited most of the operations of a Binary Search Tree. In the near Future, I plan on writing about The importance of balancing Tree, and show how to balance one. In the Meantime, If you would to see the operations of a regular Tree with animations, and a simple UI, You can check it with my tool Here.